JAVA Developer Training
32. 1916번 최소비용 구하기 본문
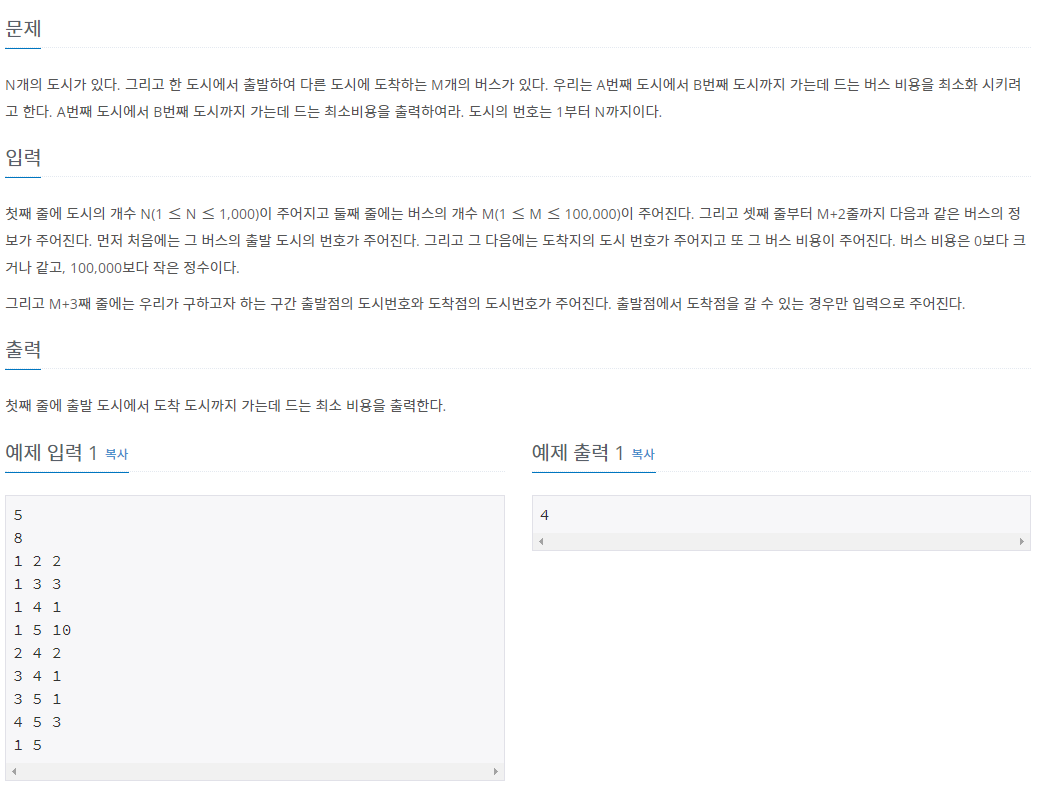
입력으로 도시의 수와 버스의 수를 입력받고
이후 시작 도시 , 도착 도시 , 거리(가중치) 를 입력받은후 원하는 도시 2곳의 위치를 입력하면 최단 거리가 출력되게 하는 문제 이다.
위 예제입력으로 보자면 아래와같다
| 첫째 줄 | 도시의 수 | 5 |
| 둘째 줄 | 버스의 수 | 8 |
| 시작 도시 | 도착 도시 | 거리(가중치) |
| 1 | 2 | 2 |
| 1 | 3 | 3 |
| 1 | 4 | 1 |
| 1 | 5 | 10 |
| 2 | 4 | 2 |
| 3 | 4 | 1 |
| 3 | 5 | 1 |
| 4 | 5 | 3 |
| 최단거리 | 시작도시,도착도시 | 1 -> 5 |
그림으로 그리면 아래와 같겠다

그렇다면 우리가 이문제에서 고려해야 할 점은 무엇인지 차근차근 살펴보자
1. 입력처리
- 각각의 입력을 도시의 수, 버스의 수, 그리고 거리를 할당해주게 해야 한다
2. 탐색 방법
2-1. 탐색을 처리하기위해 탐색하는 장기말을 하나 정의해야한다.
2-2. 장기말이 방문한 위치는 다시 오지못하도록 확인해야한다. (무한으로 빠질수 있기 때문)
2-3. 다익스트라 알고리즘을 이용한 탐색을 사용한다.
그럼 코드를 구성해보자
1. 입력처리
public class training {
//도시, 버스의수
static int City, Bus;
//시작점에서 각 정점으로가는 최단거리
static int[] D;
//방문확인
static boolean[] visited;
//거리 할당을 위한 리스트
static ArrayList<ArrayList<Node>> list;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
City = Integer.parseInt(st.nextToken());
Bus = Integer.parseInt(st.nextToken());
list = new ArrayList<>();
D = new int[City+1];
visited = new boolean[City+1];
Arrays.fill(D, Integer.MAX_VALUE);
//도시의 수만큼
for(int i=0; i<=City; i++){
list.add(new ArrayList<>());
}
//해당 선로에 거리,가중치를 설정하는작업
for(int i=0; i<=Bus; i++){
st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
list.get(start).add(new Node(end, cost));
}
st = new StringTokenizer(br.readLine());
int ansStart = Integer.parseInt(st.nextToken());
int ansEnd = Integer.parseInt(st.nextToken());
bw.write(dijkstra(ansStart,ansEnd));
bw.flush();
bw.close();
br.close();
}
}
장기말 설정
class Node implements Comparable<Node> {
int end;
int cost;
Node(int end, int cost) {
this.end = end;
this.cost = cost;
}
@Override
public int compareTo(Node o) {
return cost - o.cost;
}
}Comparable은 자바에서 기본제공해주는 인터페이스로 자기 자신과 매개변수를 비교할때 사용할 수있다.
2. 탐색
public static int dijkstra(int start,int end){
PriorityQueue<Node> pq = new PriorityQueue<>();
boolean[] visited = new boolean[City+1];
pq.offer(new Node(start, 0));
//시작지점 가중치 0
D[start] = 0;
//pq가 빌때까지
while(!pq.isEmpty()){
Node curNode = pq.poll();
// curNode는 (start,0)부터 시작
int cur = curNode.end;
// cur = start값
if(!visited[cur]){
visited[cur] =true;
for(Node node : list.get(cur)){
if(!visited[node.end] && D[cur] + node.cost < D[node.end]){
//도착한곳이 방문하지않았고 거리에 +가중치(거리)를 더했을때 기존보다 작을경우
D[node.end] = D[cur] + node.cost;
// 새 위치,가중치를 가지게된다
pq.add(new Node(node.end, D[node.end]));
}
}
}
}
return D[end];
}
결과

'백준 알고리즘' 카테고리의 다른 글
| 34. 2504번 괄호의 값 (0) | 2021.10.26 |
|---|---|
| 33. 1963번 소수 경로 (0) | 2021.10.18 |
| 30. 14502번 연구소 (0) | 2021.10.18 |
| 29. 16948번 데스나이트 (0) | 2021.10.11 |
| 28. 16928번 뱀과 사다리 게임 (0) | 2021.10.11 |




